IMO Shortlist 1985 problem 18
Dodao/la:
arhiva2. travnja 2012. Let
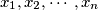
be positive numbers. Prove that
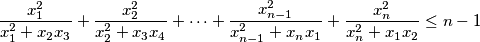
%V0
Let $x_1, x_2, \cdots , x_n$ be positive numbers. Prove that $$\frac{x_{1}^{2}}{x_{1}^{2}+x_{2}x_{3}}+\frac{x_{2}^{2}}{x_{2}^{2}+x_{3}x_{4}}+\cdots+\frac{x_{n-1}^{2}}{x_{n-1}^{2}+x_{n}x_{1}}+\frac{x_{n}^{2}}{x_{n}^{2}+x_{1}x_{2}}\leq n-1$$
Izvor: Međunarodna matematička olimpijada, shortlist 1985