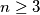
For which integers does there exist a regular -gon in the plane such that all its vertices have integer coordinates in a rectangular coordinate system?
%V0
For which integers $n \geq 3$ does there exist a regular $n$-gon in the plane such that all its vertices have integer coordinates in a rectangular coordinate system?
Izvor: Međunarodna matematička olimpijada, shortlist 1985
Školjka 
does there exist a regular 
-gon in the plane such that all its vertices have integer coordinates in a rectangular coordinate system?