IMO Shortlist 1986 problem 1
Dodao/la:
arhiva2. travnja 2012. Let
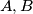
be adjacent vertices of a regular

-gon (
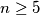
) with center
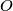
. A triangle
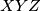
, which is congruent to and initially coincides with
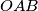
, moves in the plane in such a way that
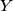
and
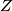
each trace out the whole boundary of the polygon, with

remaining inside the polygon. Find the locus of

.
%V0
Let $A,B$ be adjacent vertices of a regular $n$-gon ($n\ge5$) with center $O$. A triangle $XYZ$, which is congruent to and initially coincides with $OAB$, moves in the plane in such a way that $Y$ and $Z$ each trace out the whole boundary of the polygon, with $X$ remaining inside the polygon. Find the locus of $X$.
Izvor: Međunarodna matematička olimpijada, shortlist 1986