IMO Shortlist 1986 problem 2
Dodao/la:
arhiva2. travnja 2012. Let
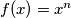
where

is a fixed positive integer and
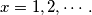
Is the decimal expansion
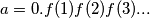
rational for any value of

?
The decimal expansion of a is defined as follows: If
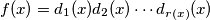
is the decimal expansion of
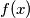
, then
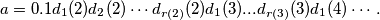
%V0
Let $f(x) = x^n$ where $n$ is a fixed positive integer and $x =1, 2, \cdots .$ Is the decimal expansion $a = 0.f (1)f(2)f(3) . . .$ rational for any value of $n$ ?
The decimal expansion of a is defined as follows: If $f(x) = d_1(x)d_2(x) \cdots d_{r(x)}(x)$ is the decimal expansion of $f(x)$, then $a = 0.1d_1(2)d_2(2) \cdots d_{r(2)}(2)d_1(3) . . . d_{r(3)}(3)d_1(4) \cdots .$
Izvor: Međunarodna matematička olimpijada, shortlist 1986