IMO Shortlist 1986 problem 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let 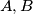 , and
, and  be three points on the edge of a circular chord such that
be three points on the edge of a circular chord such that  is due west of
is due west of  and
and  is an equilateral triangle whose side is
is an equilateral triangle whose side is 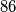 meters long. A boy swam from
meters long. A boy swam from  directly toward
directly toward  . After covering a distance of
. After covering a distance of  meters, he turned and swam westward, reaching the shore after covering a distance of
meters, he turned and swam westward, reaching the shore after covering a distance of 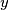 meters. If
meters. If  and
and 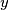 are both positive integers, determine
are both positive integers, determine 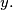
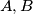 , and
, and  be three points on the edge of a circular chord such that
be three points on the edge of a circular chord such that  is due west of
is due west of  and
and  is an equilateral triangle whose side is
is an equilateral triangle whose side is 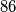 meters long. A boy swam from
meters long. A boy swam from  directly toward
directly toward  . After covering a distance of
. After covering a distance of  meters, he turned and swam westward, reaching the shore after covering a distance of
meters, he turned and swam westward, reaching the shore after covering a distance of 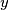 meters. If
meters. If  and
and 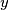 are both positive integers, determine
are both positive integers, determine 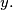
Izvor: Međunarodna matematička olimpijada, shortlist 1986
 Školjka
Školjka 
