IMO Shortlist 1986 problem 4
Dodao/la:
arhiva2. travnja 2012. Provided the equation
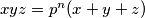
where
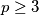
is a prime and
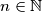
. Prove that the equation has at least
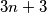
different solutions
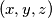
with natural numbers
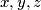
and
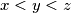
. Prove the same for
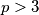
being an odd integer.
%V0
Provided the equation $xyz = p^n(x + y + z)$ where $p \geq 3$ is a prime and $n \in \mathbb{N}$. Prove that the equation has at least $3n + 3$ different solutions $(x,y,z)$ with natural numbers $x,y,z$ and $x < y < z$. Prove the same for $p > 3$ being an odd integer.
Izvor: Međunarodna matematička olimpijada, shortlist 1986