IMO Shortlist 1986 problem 7
Dodao/la:
arhiva2. travnja 2012. Let real numbers
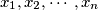
satisfy
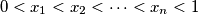
and set
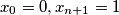
. Suppose that these numbers satisfy the following system of equations:
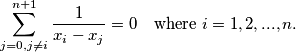
Prove that
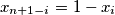
for
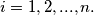
%V0
Let real numbers $x_1, x_2, \cdots , x_n$ satisfy $0 < x_1 < x_2 < \cdots< x_n < 1$ and set $x_0 = 0, x_{n+1} = 1$. Suppose that these numbers satisfy the following system of equations:
$$\sum_{j=0, j \neq i}^{n+1} \frac{1}{x_i-x_j}=0 \quad \text{where } i = 1, 2, . . ., n.$$
Prove that $x_{n+1-i} = 1- x_i$ for $i = 1, 2, . . . , n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1986