IMO Shortlist 1986 problem 10
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Three persons  , are playing the following game:
, are playing the following game:
A -element subset of the set
-element subset of the set 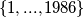 is randomly chosen, with an equal probability of each choice, where
is randomly chosen, with an equal probability of each choice, where  is a fixed positive integer less than or equal to
is a fixed positive integer less than or equal to 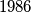 . The winner is
. The winner is 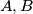 or
or  , respectively, if the sum of the chosen numbers leaves a remainder of
, respectively, if the sum of the chosen numbers leaves a remainder of 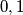 , or
, or  when divided by
when divided by  .
.
For what values of is this game a fair one? (A game is fair if the three outcomes are equally probable.)
is this game a fair one? (A game is fair if the three outcomes are equally probable.)
 , are playing the following game:
, are playing the following game:A
 -element subset of the set
-element subset of the set 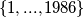 is randomly chosen, with an equal probability of each choice, where
is randomly chosen, with an equal probability of each choice, where  is a fixed positive integer less than or equal to
is a fixed positive integer less than or equal to 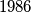 . The winner is
. The winner is 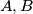 or
or  , respectively, if the sum of the chosen numbers leaves a remainder of
, respectively, if the sum of the chosen numbers leaves a remainder of 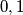 , or
, or  when divided by
when divided by  .
.For what values of
 is this game a fair one? (A game is fair if the three outcomes are equally probable.)
is this game a fair one? (A game is fair if the three outcomes are equally probable.) Izvor: Međunarodna matematička olimpijada, shortlist 1986
 Školjka
Školjka 
