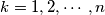
Let be the least number of distinct points in the plane such that for each there exists a straight line containing exactly of these points. Find an explicit expression for
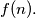
Simplified version.
Show that Where denoting the greatest integer not exceeding
%V0
Let $f(n)$ be the least number of distinct points in the plane such that for each $k = 1, 2, \cdots, n$ there exists a straight line containing exactly $k$ of these points. Find an explicit expression for $f(n).$
Simplified version.
Show that $f(n)=\left[\frac{n+1}{2}\right]\left[\frac{n+2}{2}\right].$ Where $[x]$ denoting the greatest integer not exceeding $x.$
Izvor: Međunarodna matematička olimpijada, shortlist 1986
Školjka 
be the least number of distinct points in the plane such that for each 
there exists a straight line containing exactly 
of these points. Find an explicit expression for 
![f(n)=\left[\frac{n+1}{2}\right]\left[\frac{n+2}{2}\right].](/media/m/6/0/4/60461544303c4bcc05d123404f067a5e.png)
Where ![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png)
denoting the greatest integer not exceeding 