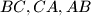
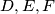
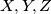
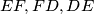
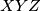
The circle inscribed in a triangle touches the sides in , respectively, and are the midpoints of , respectively. Prove that the centers of the inscribed circle and of the circles around and are collinear.
%V0
The circle inscribed in a triangle $ABC$ touches the sides $BC,CA,AB$ in $D,E, F$, respectively, and $X, Y,Z$ are the midpoints of $EF, FD,DE$, respectively. Prove that the centers of the inscribed circle and of the circles around $XYZ$ and $ABC$ are collinear.
Izvor: Međunarodna matematička olimpijada, shortlist 1986
Školjka 
touches the sides 
in 
, respectively, and 
are the midpoints of 
, respectively. Prove that the centers of the inscribed circle and of the circles around 
and