IMO Shortlist 1986 problem 15
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a convex quadrilateral whose vertices do not lie on a circle. Let
be a convex quadrilateral whose vertices do not lie on a circle. Let 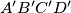 be a quadrangle such that
be a quadrangle such that 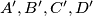 are the centers of the circumcircles of triangles
are the centers of the circumcircles of triangles 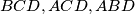 , and
, and  . We write
. We write 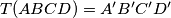 . Let us define
. Let us define 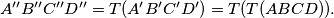
(a) Prove that and
and 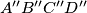 are similar.
are similar.
(b) The ratio of similitude depends on the size of the angles of . Determine this ratio.
. Determine this ratio.
 be a convex quadrilateral whose vertices do not lie on a circle. Let
be a convex quadrilateral whose vertices do not lie on a circle. Let 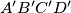 be a quadrangle such that
be a quadrangle such that 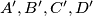 are the centers of the circumcircles of triangles
are the centers of the circumcircles of triangles 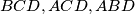 , and
, and  . We write
. We write 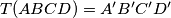 . Let us define
. Let us define 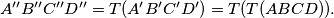
(a) Prove that
 and
and 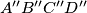 are similar.
are similar.(b) The ratio of similitude depends on the size of the angles of
 . Determine this ratio.
. Determine this ratio. Izvor: Međunarodna matematička olimpijada, shortlist 1986
 Školjka
Školjka 
