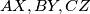
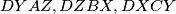
Let be three cevians concurrent at an interior point of a triangle . Prove that if two of the quadrangles are circumscribable, so is the third.
%V0
Let $AX,BY,CZ$ be three cevians concurrent at an interior point $D$ of a triangle $ABC$. Prove that if two of the quadrangles $DY AZ,DZBX,DXCY$ are circumscribable, so is the third.
Izvor: Međunarodna matematička olimpijada, shortlist 1986
Školjka 
be three cevians concurrent at an interior point 
of a triangle 
. Prove that if two of the quadrangles 
are circumscribable, so is the third.