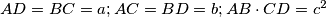
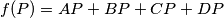
A tetrahedron is given such that . Let , where is an arbitrary point in space. Compute the least value of
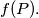
%V0
A tetrahedron $ABCD$ is given such that $AD = BC = a; AC = BD = b; AB\cdot CD = c^2$. Let $f(P) = AP + BP + CP + DP$, where $P$ is an arbitrary point in space. Compute the least value of $f(P).$
Izvor: Međunarodna matematička olimpijada, shortlist 1986
Školjka 
is given such that 
. Let 
, where 
is an arbitrary point in space. Compute the least value of 