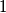
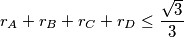
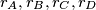
Let be a tetrahedron having each sum of opposite sides equal to . Prove that where are the inradii of the faces, equality holding only if is regular.
%V0
Let $ABCD$ be a tetrahedron having each sum of opposite sides equal to $1$. Prove that
$$r_A + r_B + r_C + r_D \leq \frac{\sqrt 3}{3}$$
where $r_A, r_B, r_C, r_D$ are the inradii of the faces, equality holding only if $ABCD$ is regular.
Izvor: Međunarodna matematička olimpijada, shortlist 1986
Školjka 
be a tetrahedron having each sum of opposite sides equal to 
. Prove that
are the inradii of the faces, equality holding only if