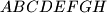
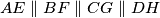
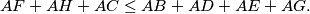
Let be a parallelepiped with . Prove the inequality In what cases does equality hold?
Proposed by France.
%V0
Let $ABCDEFGH$ be a parallelepiped with $AE \parallel BF \parallel CG \parallel DH$. Prove the inequality
$$AF + AH + AC \leq AB + AD + AE + AG.$$
In what cases does equality hold?
Proposed by France.
Izvor: Međunarodna matematička olimpijada, shortlist 1987
Školjka 
be a parallelepiped with 
. Prove the inequality