IMO Shortlist 1987 problem 6
Dodao/la:
arhiva2. travnja 2012. Show that if

are the lengths of the sides of a triangle and if
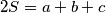
, then
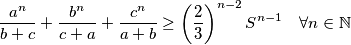
Proposed by Greece.
%V0
Show that if $a, b, c$ are the lengths of the sides of a triangle and if $2S = a + b + c$, then
$$\frac{a^n}{b+c} + \frac{b^n}{c+a} +\frac{c^n}{a+b} \geq \left(\dfrac 23 \right)^{n-2}S^{n-1} \quad \forall n \in \mathbb N$$
Proposed by Greece.
Izvor: Međunarodna matematička olimpijada, shortlist 1987