IMO Shortlist 1987 problem 12
Dodao/la:
arhiva2. travnja 2012. Given a nonequilateral triangle

, the vertices listed counterclockwise, find the locus of the centroids of the equilateral triangles
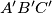
(the vertices listed counterclockwise) for which the triples of points
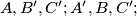
and
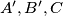
are collinear.
Proposed by Poland.
%V0
Given a nonequilateral triangle $ABC$, the vertices listed counterclockwise, find the locus of the centroids of the equilateral triangles $A'B'C'$ (the vertices listed counterclockwise) for which the triples of points $A,B', C'; A',B, C';$ and $A',B', C$ are collinear.
Proposed by Poland.
Izvor: Međunarodna matematička olimpijada, shortlist 1987