IMO Shortlist 1987 problem 18
Dodao/la:
arhiva2. travnja 2012. For any integer
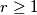
, determine the smallest integer
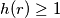
such that for any partition of the set
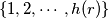
into

classes, there are integers
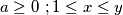
, such that
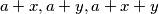
belong to the same class.
Proposed by Romania
%V0
For any integer $r \geq 1$, determine the smallest integer $h(r) \geq 1$ such that for any partition of the set $\{1, 2, \cdots, h(r)\}$ into $r$ classes, there are integers $a \geq 0 \ ; 1 \leq x \leq y$, such that $a + x, a + y, a + x + y$ belong to the same class.
Proposed by Romania
Izvor: Međunarodna matematička olimpijada, shortlist 1987