IMO Shortlist 1988 problem 1
Dodao/la:
arhiva2. travnja 2012. An integer sequence is defined by
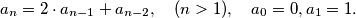
Prove that
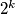
divides

if and only if
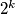
divides
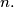
%V0
An integer sequence is defined by
$$a_n = 2 \cdot a_{n-1} + a_{n-2}, \quad (n > 1), \quad a_0 = 0, a_1 = 1.$$
Prove that $2^k$ divides $a_n$ if and only if $2^k$ divides $n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1988