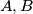
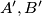
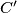
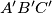
The triangle is inscribed in a circle. The interior bisectors of the angles and meet the circle again at and respectively. Prove that the area of triangle is greater than or equal to the area of triangle
%V0
The triangle $ABC$ is inscribed in a circle. The interior bisectors of the angles $A,B$ and $C$ meet the circle again at $A', B'$ and $C'$ respectively. Prove that the area of triangle $A'B'C'$ is greater than or equal to the area of triangle $ABC.$
Izvor: Međunarodna matematička olimpijada, shortlist 1988
Školjka 
is inscribed in a circle. The interior bisectors of the angles 
and 
meet the circle again at 
and 
respectively. Prove that the area of triangle 
is greater than or equal to the area of triangle 