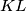
In a given tedrahedron let and be the centres of edges and respectively. Prove that every plane that contains the line divides the tedrahedron into two parts of equal volume.
%V0
In a given tedrahedron $ABCD$ let $K$ and $L$ be the centres of edges $AB$ and $CD$ respectively. Prove that every plane that contains the line $KL$ divides the tedrahedron into two parts of equal volume.
Izvor: Međunarodna matematička olimpijada, shortlist 1988
Školjka 
let 
and 
be the centres of edges 
and 
respectively. Prove that every plane that contains the line 
divides the tedrahedron into two parts of equal volume.