IMO Shortlist 1988 problem 12
Dodao/la:
arhiva2. travnja 2012. In a triangle
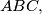
choose any points
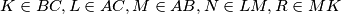
and
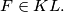
If
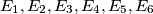
and

denote the areas of the triangles
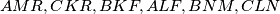
and

respectively, show that
![E \geq 8 \cdot \sqrt [6]{E_1 E_2 E_3 E_4 E_5 E_6}.](/media/m/0/c/4/0c43bf041ee58132ee5e9bad759ee36f.png)
%V0
In a triangle $ABC,$ choose any points $K \in BC, L \in AC, M \in AB, N \in LM, R \in MK$ and $F \in KL.$ If $E_1, E_2, E_3, E_4, E_5, E_6$ and $E$ denote the areas of the triangles $AMR, CKR, BKF, ALF, BNM, CLN$ and $ABC$ respectively, show that
$$E \geq 8 \cdot \sqrt [6]{E_1 E_2 E_3 E_4 E_5 E_6}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1988