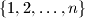
Find the least natural number such that, if the set is arbitrarily divided into two non-intersecting subsets, then one of the subsets contains 3 distinct numbers such that the product of two of them equals the third.
%V0
Find the least natural number $n$ such that, if the set $\{1,2, \ldots, n\}$ is arbitrarily divided into two non-intersecting subsets, then one of the subsets contains 3 distinct numbers such that the product of two of them equals the third.
Izvor: Međunarodna matematička olimpijada, shortlist 1988
Školjka 
such that, if the set 
is arbitrarily divided into two non-intersecting subsets, then one of the subsets contains 3 distinct numbers such that the product of two of them equals the third.