IMO Shortlist 1988 problem 21
Dodao/la:
arhiva2. travnja 2012. Forty-nine students solve a set of 3 problems. The score for each problem is a whole number of points from 0 to 7. Prove that there exist two students

and

such that, for each problem,

will score at least as many points as
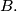
%V0
Forty-nine students solve a set of 3 problems. The score for each problem is a whole number of points from 0 to 7. Prove that there exist two students $A$ and $B$ such that, for each problem, $A$ will score at least as many points as $B.$
Izvor: Međunarodna matematička olimpijada, shortlist 1988