IMO Shortlist 1988 problem 27
Dodao/la:
arhiva2. travnja 2012. Let

be an acute-angled triangle. Let

be any line in the plane of the triangle

. Denote by
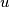
,

,

the lengths of the perpendiculars to

from

,

,

respectively. Prove the inequality
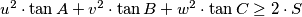
, where

is the area of the triangle

. Determine the lines

for which equality holds.
%V0
Let $ABC$ be an acute-angled triangle. Let $L$ be any line in the plane of the triangle $ABC$. Denote by $u$, $v$, $w$ the lengths of the perpendiculars to $L$ from $A$, $B$, $C$ respectively. Prove the inequality $u^2\cdot\tan A + v^2\cdot\tan B + w^2\cdot\tan C\geq 2\cdot S$, where $S$ is the area of the triangle $ABC$. Determine the lines $L$ for which equality holds.
Izvor: Međunarodna matematička olimpijada, shortlist 1988