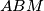
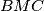
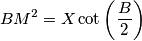
A point is chosen on the side of the triangle in such a way that the radii of the circles inscribed in the triangles and are equal. Prove that where X is the area of triangle
%V0
A point $M$ is chosen on the side $AC$ of the triangle $ABC$ in such a way that the radii of the circles inscribed in the triangles $ABM$ and $BMC$ are equal. Prove that
$$BM^{2} = X \cot \left( \frac {B}{2}\right)$$
where X is the area of triangle $ABC.$
Izvor: Međunarodna matematička olimpijada, shortlist 1988
Školjka 
is chosen on the side 
of the triangle 
in such a way that the radii of the circles inscribed in the triangles 
and 
are equal. Prove that 
