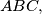
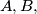
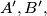
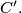
For a triangle let be its circumcircle with radius The bisectors of the inner angles and of the triangle intersect respectively the circle again at points and Prove the inequality
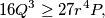
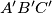
where and are the areas of the triangles and respectively.
%V0
For a triangle $ABC,$ let $k$ be its circumcircle with radius $r.$ The bisectors of the inner angles $A, B,$ and $C$ of the triangle intersect respectively the circle $k$ again at points $A', B',$ and $C'.$ Prove the inequality
$$16Q^3 \geq 27 r^4 P,$$
where $Q$ and $P$ are the areas of the triangles $A'B'C'$ and $ABC$ respectively.
Izvor: Međunarodna matematička olimpijada, shortlist 1989
Školjka 
let 
be its circumcircle with radius 
The bisectors of the inner angles 
and 
of the triangle intersect respectively the circle 
and 
Prove the inequality
and 
are the areas of the triangles 
and 
respectively.