IMO Shortlist 1989 problem 9
Dodao/la:
arhiva2. travnja 2012. 
there exists uniquely determined integers
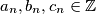
such
![\left(1 + 4 \cdot \sqrt[3]{2} - 4 \cdot \sqrt[3]{4} \right)^n = a_n + b_n \cdot \sqrt[3]{2} + c_n \cdot \sqrt[3]{4}.](/media/m/9/7/8/97803f4eeaf0e47fd00e9b1ea8ad4f40.png)
Prove that
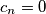
implies
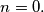
%V0
$\forall n > 0, n \in \mathbb{Z},$ there exists uniquely determined integers $a_n, b_n, c_n \in \mathbb{Z}$ such
$$\left(1 + 4 \cdot \sqrt[3]{2} - 4 \cdot \sqrt[3]{4} \right)^n = a_n + b_n \cdot \sqrt[3]{2} + c_n \cdot \sqrt[3]{4}.$$
Prove that $c_n = 0$ implies $n = 0.$
Izvor: Međunarodna matematička olimpijada, shortlist 1989