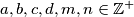
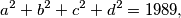
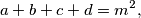
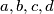
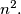
Let such that and the largest of is Determine, with proof, the values of and
%V0
Let $a, b, c, d,m, n \in \mathbb{Z}^+$ such that $$a^2+b^2+c^2+d^2 = 1989,$$
$$a+b+c+d = m^2,$$ and the largest of $a, b, c, d$ is $n^2.$ Determine, with proof, the values of $m$ and $n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1989
Školjka 
such that 
and the largest of 
is 
Determine, with proof, the values of 
and 