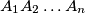
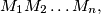
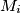
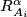
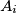
Given a convex polygon with area and a point in the same plane, determine the area of polygon where is the image of under rotation around by
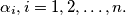
%V0
Given a convex polygon $A_1A_2 \ldots A_n$ with area $S$ and a point $M$ in the same plane, determine the area of polygon $M_1M_2 \ldots M_n,$ where $M_i$ is the image of $M$ under rotation $R^{\alpha}_{A_i}$ around $A_i$ by $\alpha_i, i = 1, 2, \ldots, n.$
Izvor: Međunarodna matematička olimpijada, shortlist 1989
Školjka 
with area 
and a point 
in the same plane, determine the area of polygon 
where 
is the image of 
around 
by 