IMO Shortlist 1989 problem 19
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 A natural number is written in each square of an 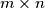 chess board. The allowed move is to add an integer
chess board. The allowed move is to add an integer  to each of two adjacent numbers in such a way that non-negative numbers are obtained. (Two squares are adjacent if they have a common side.) Find a necessary and sufficient condition for it to be possible for all the numbers to be zero after finitely many operations.
to each of two adjacent numbers in such a way that non-negative numbers are obtained. (Two squares are adjacent if they have a common side.) Find a necessary and sufficient condition for it to be possible for all the numbers to be zero after finitely many operations.
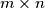 chess board. The allowed move is to add an integer
chess board. The allowed move is to add an integer  to each of two adjacent numbers in such a way that non-negative numbers are obtained. (Two squares are adjacent if they have a common side.) Find a necessary and sufficient condition for it to be possible for all the numbers to be zero after finitely many operations.
to each of two adjacent numbers in such a way that non-negative numbers are obtained. (Two squares are adjacent if they have a common side.) Find a necessary and sufficient condition for it to be possible for all the numbers to be zero after finitely many operations. Izvor: Međunarodna matematička olimpijada, shortlist 1989
 Školjka
Školjka 
