IMO Shortlist 1989 problem 21
Dodao/la:
arhiva2. travnja 2012. Prove that the intersection of a plane and a regular tetrahedron can be an obtuse-angled triangle and that the obtuse angle in any such triangle is always smaller than
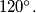
%V0
Prove that the intersection of a plane and a regular tetrahedron can be an obtuse-angled triangle and that the obtuse angle in any such triangle is always smaller than $120^{\circ}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1989