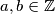
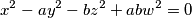
Let which are not perfect squares. Prove that if has a nontrivial solution in integers, then so does
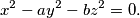
%V0
Let $a, b \in \mathbb{Z}$ which are not perfect squares. Prove that if $$x^2 - ay^2 - bz^2 + abw^2 = 0$$ has a nontrivial solution in integers, then so does $$x^2 - ay^2 - bz^2 = 0.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1989
Školjka 
which are not perfect squares. Prove that if 
has a nontrivial solution in integers, then so does 