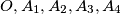
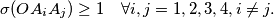
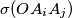
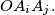
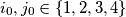
Consider in a plane the points such that where is the area of triangle Prove that there exists at least one pair such that
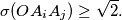
%V0
Consider in a plane $P$ the points $O,A_1,A_2,A_3,A_4$ such that $$\sigma(OA_iA_j) \geq 1 \quad \forall i, j = 1, 2, 3, 4, i \neq j.$$ where $\sigma(OA_iA_j)$ is the area of triangle $OA_iA_j.$ Prove that there exists at least one pair $i_0, j_0 \in \{1, 2, 3, 4\}$ such that $$\sigma(OA_iA_j) \geq \sqrt{2}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1989
Školjka 
the points 
such that 
where 
is the area of triangle 
Prove that there exists at least one pair 
such that 