IMO Shortlist 1990 problem 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Given  countries with three representatives each,
countries with three representatives each,  committees
committees 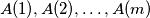 are called a cycle if
are called a cycle if
(i) each committee has members, one from each country;
members, one from each country;
(ii) no two committees have the same membership;
(iii) for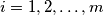 , committee
, committee 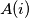 and committee
and committee 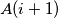 have no member in common, where
have no member in common, where 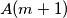 denotes
denotes 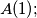
(iv) if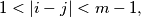 then committees
then committees 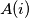 and
and 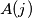 have at least one member in common.
have at least one member in common.
Is it possible to have a cycle of 1990 committees with 11 countries?
 countries with three representatives each,
countries with three representatives each,  committees
committees 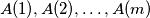 are called a cycle if
are called a cycle if (i) each committee has
 members, one from each country;
members, one from each country; (ii) no two committees have the same membership;
(iii) for
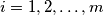 , committee
, committee 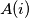 and committee
and committee 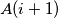 have no member in common, where
have no member in common, where 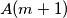 denotes
denotes 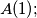
(iv) if
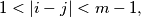 then committees
then committees 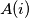 and
and 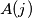 have at least one member in common.
have at least one member in common. Is it possible to have a cycle of 1990 committees with 11 countries?
Izvor: Međunarodna matematička olimpijada, shortlist 1990
 Školjka
Školjka 
