IMO Shortlist 1990 problem 4
Dodao/la:
arhiva2. travnja 2012. Assume that the set of all positive integers is decomposed into

(disjoint) subsets
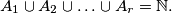
Prove that one of them, say
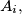
has the following property: There exists a positive

such that for any

one can find numbers
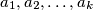
in
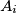
with
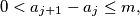
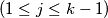
.
%V0
Assume that the set of all positive integers is decomposed into $r$ (disjoint) subsets $A_1 \cup A_2 \cup \ldots \cup A_r = \mathbb{N}.$ Prove that one of them, say $A_i,$ has the following property: There exists a positive $m$ such that for any $k$ one can find numbers $a_1, a_2, \ldots, a_k$ in $A_i$ with $0 < a_{j + 1} - a_j \leq m,$ $(1 \leq j \leq k - 1)$.
Izvor: Međunarodna matematička olimpijada, shortlist 1990