IMO Shortlist 1990 problem 12
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a triangle, and let the angle bisectors of its angles
be a triangle, and let the angle bisectors of its angles 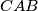 and
and  meet the sides
meet the sides  and
and  at the points
at the points  and
and  , respectively. The lines
, respectively. The lines  and
and 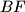 meet the line through the point
meet the line through the point  parallel to
parallel to  at the points
at the points  and
and  respectively, and we have
respectively, and we have 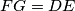 . Prove that
. Prove that 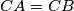 .
.
Original formulation:
Let be a triangle and
be a triangle and  the line through
the line through  parallel to the side
parallel to the side 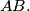 Let the internal bisector of the angle at
Let the internal bisector of the angle at  meet the side
meet the side  at
at  and the line
and the line  at
at  and let the internal bisector of the angle at
and let the internal bisector of the angle at  meet the side
meet the side  at
at  and the line
and the line  at
at 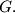 If
If 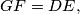 prove that
prove that 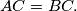
 be a triangle, and let the angle bisectors of its angles
be a triangle, and let the angle bisectors of its angles 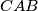 and
and  meet the sides
meet the sides  and
and  at the points
at the points  and
and  , respectively. The lines
, respectively. The lines  and
and 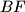 meet the line through the point
meet the line through the point  parallel to
parallel to  at the points
at the points  and
and  respectively, and we have
respectively, and we have 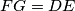 . Prove that
. Prove that 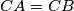 .
. Original formulation:
Let
 be a triangle and
be a triangle and  the line through
the line through  parallel to the side
parallel to the side 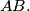 Let the internal bisector of the angle at
Let the internal bisector of the angle at  meet the side
meet the side  at
at  and the line
and the line  at
at  and let the internal bisector of the angle at
and let the internal bisector of the angle at  meet the side
meet the side  at
at  and the line
and the line  at
at 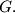 If
If 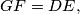 prove that
prove that 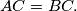
Izvor: Međunarodna matematička olimpijada, shortlist 1990
 Školjka
Školjka 
