IMO Shortlist 1990 problem 14
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 In the coordinate plane a rectangle with vertices 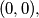
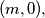
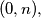
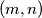 is given where both
is given where both  and
and  are odd integers. The rectangle is partitioned into triangles in such a way that
are odd integers. The rectangle is partitioned into triangles in such a way that
(i) each triangle in the partition has at least one side (to be called a “good” side) that lies on a line of the form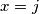 or
or 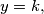 where
where  and
and  are integers, and the altitude on this side has length 1;
are integers, and the altitude on this side has length 1;
(ii) each “bad” side (i.e., a side of any triangle in the partition that is not a “good” one) is a common side of two triangles in the partition.
Prove that there exist at least two triangles in the partition each of which has two good sides.
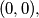
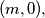
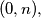
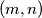 is given where both
is given where both  and
and  are odd integers. The rectangle is partitioned into triangles in such a way that
are odd integers. The rectangle is partitioned into triangles in such a way that (i) each triangle in the partition has at least one side (to be called a “good” side) that lies on a line of the form
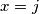 or
or 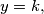 where
where  and
and  are integers, and the altitude on this side has length 1;
are integers, and the altitude on this side has length 1; (ii) each “bad” side (i.e., a side of any triangle in the partition that is not a “good” one) is a common side of two triangles in the partition.
Prove that there exist at least two triangles in the partition each of which has two good sides.
Izvor: Međunarodna matematička olimpijada, shortlist 1990
 Školjka
Školjka 
