IMO Shortlist 1990 problem 17
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Unit cubes are made into beads by drilling a hole through them along a diagonal. The beads are put on a string in such a way that they can move freely in space under the restriction that the vertices of two neighboring cubes are touching. Let  be the beginning vertex and
be the beginning vertex and  be the end vertex. Let there be
be the end vertex. Let there be 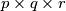 cubes on the string
cubes on the string 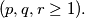
(a) Determine for which values of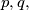 and
and  it is possible to build a block with dimensions
it is possible to build a block with dimensions 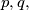 and
and  Give reasons for your answers.
Give reasons for your answers.
(b) The same question as (a) with the extra condition that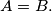
 be the beginning vertex and
be the beginning vertex and  be the end vertex. Let there be
be the end vertex. Let there be 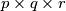 cubes on the string
cubes on the string 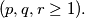
(a) Determine for which values of
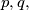 and
and  it is possible to build a block with dimensions
it is possible to build a block with dimensions 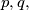 and
and  Give reasons for your answers.
Give reasons for your answers. (b) The same question as (a) with the extra condition that
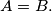
Izvor: Međunarodna matematička olimpijada, shortlist 1990
 Školjka
Školjka 
