IMO Shortlist 1990 problem 24
Dodao/la:
arhiva2. travnja 2012. Let
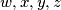
are non-negative reals such that
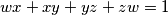
. Show that
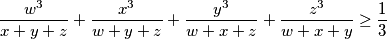
.
%V0
Let $w, x, y, z$ are non-negative reals such that $wx + xy + yz + zw = 1$. Show that
$$\frac {w^3}{x + y + z} + \frac {x^3}{w + y + z} + \frac {y^3}{w + x + z} + \frac {z^3}{w + x + y}\geq \frac {1}{3}$$.
Izvor: Međunarodna matematička olimpijada, shortlist 1990