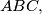
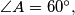
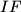
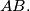
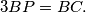
In the triangle with a parallel to is drawn through the incenter of the triangle, where lies on the side The point on the side is such that Show that
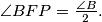
%V0
In the triangle $ABC,$ with $\angle A = 60 ^{\circ},$ a parallel $IF$ to $AC$ is drawn through the incenter $I$ of the triangle, where $F$ lies on the side $AB.$ The point $P$ on the side $BC$ is such that $3BP = BC.$ Show that $\angle BFP = \frac{\angle B}{2}.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
with 
a parallel 
to 
is drawn through the incenter 
of the triangle, where 
lies on the side 
The point 
on the side 
is such that 
Show that 