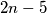
be a set of points in the plane. No three points of are collinear. Prove that there exists a set containing points satisfying the following condition: In the interior of every triangle whose three vertices are elements of lies a point that is an element of
%V0
$S$ be a set of $n$ points in the plane. No three points of $S$ are collinear. Prove that there exists a set $P$ containing $2n - 5$ points satisfying the following condition: In the interior of every triangle whose three vertices are elements of $S$ lies a point that is an element of $P.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
be a set of 
points in the plane. No three points of 
containing 
points satisfying the following condition: In the interior of every triangle whose three vertices are elements of 