Školjka IMO Shortlist 1991 problem 8
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0
In the plane we are given a set 
of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of 
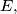there exist at least 1593 other points of to which it is joined by a path. Show that there exist six points of every pair of which are joined by a path.
Alternative version: Is it possible to find a set of 1991 points in the plane and paths joining certain pairs of the points in such that every point of is joined with a path to at least 1592 other points of 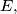and in every subset of six points of there exist at least two points that are not joined?
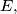of 1991 points, and certain pairs of these points are joined with a path. We suppose that for every point of there exist at least 1593 other points of to which it is joined by a path. Show that there exist six points of every pair of which are joined by a path. Alternative version: Is it possible to find a set
of 1991 points in the plane and paths joining certain pairs of the points in such that every point of is joined with a path to at least 1592 other points of 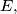and in every subset of six points of there exist at least two points that are not joined? Izvor: Međunarodna matematička olimpijada, shortlist 1991