IMO Shortlist 1991 problem 9
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Suppose 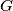 is a connected graph with
is a connected graph with 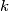 edges. Prove that it is possible to label the edges
edges. Prove that it is possible to label the edges 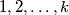 in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1.
in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1.
Graph-DefinitionA graph consists of a set of points, called vertices, together with a set of edges joining certain pairs of distinct vertices. Each pair of vertices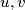 belongs to at most one edge. The graph
belongs to at most one edge. The graph  is connected if for each pair of distinct vertices
is connected if for each pair of distinct vertices 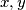 there is some sequence of vertices
there is some sequence of vertices 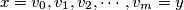 such that each pair
such that each pair 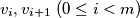 is joined by an edge of
is joined by an edge of 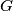 .
.
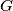 is a connected graph with
is a connected graph with 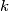 edges. Prove that it is possible to label the edges
edges. Prove that it is possible to label the edges 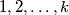 in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1.
in such a way that at each vertex which belongs to two or more edges, the greatest common divisor of the integers labeling those edges is equal to 1. Graph-DefinitionA graph consists of a set of points, called vertices, together with a set of edges joining certain pairs of distinct vertices. Each pair of vertices
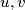 belongs to at most one edge. The graph
belongs to at most one edge. The graph  is connected if for each pair of distinct vertices
is connected if for each pair of distinct vertices 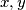 there is some sequence of vertices
there is some sequence of vertices 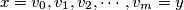 such that each pair
such that each pair 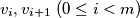 is joined by an edge of
is joined by an edge of 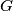 .
. Izvor: Međunarodna matematička olimpijada, shortlist 1991
 Školjka
Školjka 
