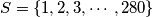
Let . Find the smallest integer such that each -element subset of contains five numbers which are pairwise relatively prime.
%V0
Let $S = \{1,2,3,\cdots ,280\}$. Find the smallest integer $n$ such that each $n$-element subset of $S$ contains five numbers which are pairwise relatively prime.
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
. Find the smallest integer 
such that each 
contains five numbers which are pairwise relatively prime.