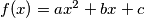
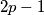
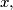
Let be integers and an odd prime number. Prove that if is a perfect square for consecutive integer values of then divides
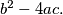
%V0
Let $a, b, c$ be integers and $p$ an odd prime number. Prove that if $f(x) = ax^2 + bx + c$ is a perfect square for $2p - 1$ consecutive integer values of $x,$ then $p$ divides $b^2 - 4ac.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
be integers and 
an odd prime number. Prove that if 
is a perfect square for 
consecutive integer values of 
then 