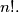
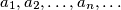
Let be the last nonzero digit in the decimal representation of the number Does the sequence become periodic after a finite number of terms?
%V0
Let $a_n$ be the last nonzero digit in the decimal representation of the number $n!.$ Does the sequence $a_1, a_2, \ldots, a_n, \ldots$ become periodic after a finite number of terms?
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
be the last nonzero digit in the decimal representation of the number 
Does the sequence 
become periodic after a finite number of terms?