IMO Shortlist 1991 problem 15
Dodao/la:
arhiva2. travnja 2012. Let
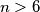
be an integer and
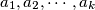
be all the natural numbers less than

and relatively prime to

. If
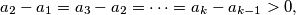
prove that
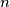
must be either a prime number or a power of
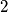
.
%V0
Let $\,n > 6\,$ be an integer and $\,a_{1},a_{2},\cdots ,a_{k}\,$ be all the natural numbers less than $n$ and relatively prime to $n$. If
$$a_{2} - a_{1} = a_{3} - a_{2} = \cdots = a_{k} - a_{k - 1} > 0,$$
prove that $\,n\,$ must be either a prime number or a power of $\,2$.
Izvor: Međunarodna matematička olimpijada, shortlist 1991