IMO Shortlist 1991 problem 19
Dodao/la:
arhiva2. travnja 2012. Let

be the positive root of the equation
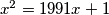
. For natural numbers

and

define
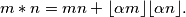
Prove that for all natural numbers

,

, and

,
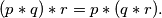
%V0
Let $\alpha$ be the positive root of the equation $x^{2} = 1991x + 1$. For natural numbers $m$ and $n$ define
$$m*n = mn + \lfloor\alpha m \rfloor \lfloor \alpha n\rfloor.$$
Prove that for all natural numbers $p$, $q$, and $r$,
$$(p*q)*r = p*(q*r).$$
Izvor: Međunarodna matematička olimpijada, shortlist 1991