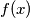
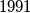
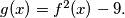
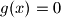
Let be a monic polynomial of degree with integer coefficients. Define Show that the number of distinct integer solutions of cannot exceed
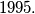
%V0
Let $f(x)$ be a monic polynomial of degree $1991$ with integer coefficients. Define $g(x) = f^2(x) - 9.$ Show that the number of distinct integer solutions of $g(x) = 0$ cannot exceed $1995.$
Izvor: Međunarodna matematička olimpijada, shortlist 1991
Školjka 
be a monic polynomial of degree 
with integer coefficients. Define 
Show that the number of distinct integer solutions of 
cannot exceed 